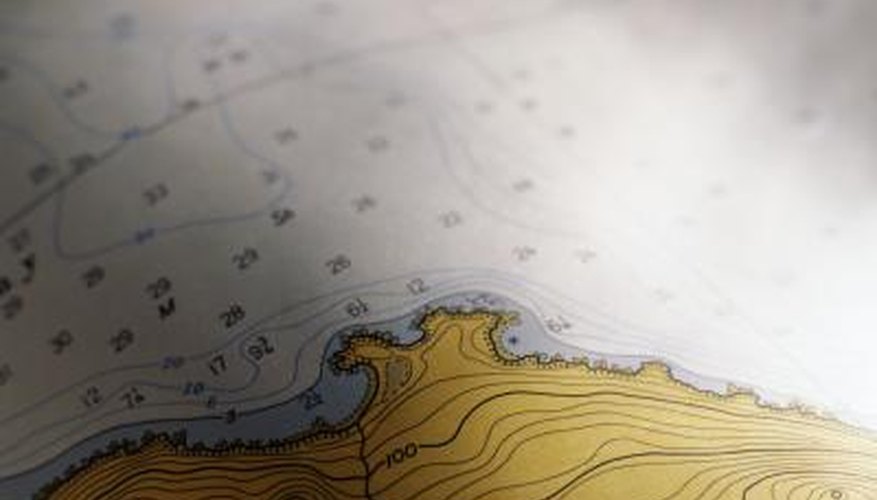
An important feature of topographic maps is the use of contour lines to note elevation. A contour line connects points of similar elevation. On topographic maps they are indicated by brown lines and come in three types. Index contour lines are labeled with their elevation value and are dark brown. Intermediate contour lines are lighter brown and are placed at equal elevation intervals between index contour lines. Supplementary contour lines appear at half the elevation interval of an intermediate contour line and are used in areas where there is gradual change in elevation.
Items you will need
Topographic Map
Pencil
Step 1
Find the location of the elevation to be determined on the map.
Step 2
Locate the nearest index contour line to your location. The value on the line is the elevation of that contour line.
Step 3
Determine the direction of the slope (aspect) from the index contour line to your location by drawing an arrow from the index contour line to the next higher elevation contour line. If the arrow is pointing toward the contour lines around your location, your location is a higher elevation than the index contour line. If the arrow is pointing away from the contour lines around your location, your location is a lower elevation than the index contour line.
Step 4
Count the number of contour lines between the index contour line and your location. Add 0.5 to your count if a supplementary contour line is between your location and the nearest intermediate contour line.
Step 5
Find the contour interval located below the bar scale on the bottom margin of the map. The contour interval gives the change in elevation for two adjacent contour lines.
Step 6
Multiply the contour interval by the number of intermediate contour lines between your location and the index contour line.
Step 7
Add the product to the value of the nearest contour interval if your location is higher than the index contour line. Subtract if your location is lower than the nearest index contour line.
References
- Reading Topographic Maps and Making Calculations
- “FM3-25.26 Map Reading and Land Navigation;” US Army; 2001
Writer Bio
David Chandler has been a freelance writer since 2006 whose work has appeared in various print and online publications. A former reconnaissance Marine, he is an active hiker, diver, kayaker, sailor and angler. He has traveled extensively and holds a bachelor's degree from the University of South Florida where he was educated in international studies and microbiology.



